Median algebra
In mathematics, a median algebra is a set with a ternary operation < x,y,z > satisfying a set of axioms which generalise the notion of median or majority function, as a Boolean function.
The axioms are
- < x,y,y > = y
- < x,y,z > = < z,x,y >
- < x,y,z > = < x,z,y >
- < < x,w,y > ,w,z > = < x,w, < y,w,z > >
The second and third axioms imply commutativity: it is possible (but not easy) to show that in the presence of the other three, axiom (3) is redundant. The fourth axiom implies associativity. There are other possible axiom systems: for example the two
- < x,y,y > = y
- < u,v, < u,w,x > > = < u,x, < w,u,v > >
also suffice.
In a Boolean algebra, or more generally a distributive lattice, the median function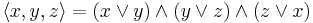 
satisfies these axioms, so that every Boolean algebra and every distributive lattice forms a median algebra.
Birkhoff and Kiss showed that a median algebra with elements 0 and 1 satisfying < 0,x,1 > = x is a distributive lattice.
Relation to median graphs
A median graph is an undirected graph in which for every three vertices x, y, and z there is a unique vertex < x,y,z > that belongs to shortest paths between any two of x, y, and z. If this is the case, then the operation < x,y,z > defines a median algebra having the vertices of the graph as its elements.
Conversely, in any median algebra, one may define an interval [x, z] to be the set of elements y such that < x,y,z > = y. One may define a graph from a median algebra by creating a vertex for each algebra element and an edge for each pair (x, z) such that the interval [x, z] contains no other elements. If the algebra has the property that every interval is finite, then this graph is a median graph, and it accurately represents the algebra in that the median operation defined by shortest paths on the graph coincides with the algebra's original median operation.
References
- Birkhoff, Garrett; Kiss, S.A. (1947). "A ternary operation in distributive lattices". Bull. Amer. Math. Soc. 53 (8): 749–752. doi:10.1090/S0002-9904-1947-08864-9.
- Isbell, John R. (August 1980). "Median algebra". Trans. Amer. Math. Soc. (American Mathematical Society) 260 (2): 319–362. doi:10.2307/1998007. JSTOR 1998007.
- Knuth, Donald E. (2008). Introduction to combinatorial algorithms and Boolean functions. The Art of Computer Programming. 4.0. Upper Saddle River, NJ: Addison-Wesley. pp. 64–74. ISBN 0-321-53496-4.